相対性理論のアインシュタインも絶賛した
複利（指数関数的成長）とは？

相対性理論で有名なアインシュタインの名を知らない人はいないでしょう。
そのアインシュタインが、実はこんな名言を残しています。

数学における最も偉大な発見は複利の力である。
　　　　　　　　　　　　　　　アインシュタイン（物理学者）

まずは、この複利の仕組みを簡単にご説明します。

銀行預金の利息計算で、単利、複利という言葉をよく聞きますが、
それらは、次のような意味です。

単利・・・利息を受け取り元金に再投資しない
複利・・・利息を受け取らず元金に組み入れていく

どういうことかというと…

単利運用の例

たとえば、ちょっと現実的ではありませんが、
わかりやすく毎年１０％の利息がもらえる定期預金があったとします。

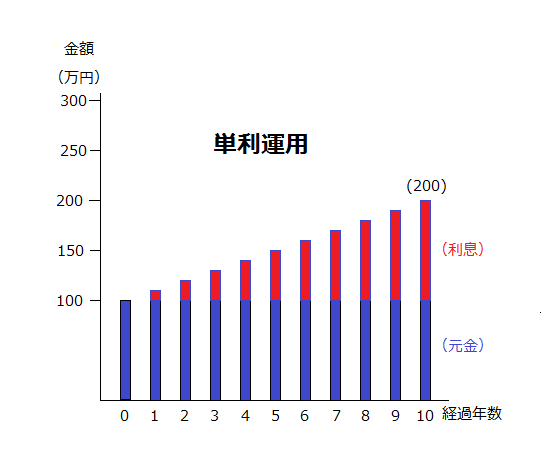
１００万円の元金を預けた場合、単利と複利では
どれくらいの違いが出るでしょうか。

単利運用の場合、
毎年もらえる１０％の利息を受け取り、
元金に再投資しません。
毎年１０万円の利息×１０年で
１００万円増えます。

受け取った利息を手元に置いて
再投資しなければ、
元金と合わせて１０年後に
２００万円になります。

　１００万円 ＋ １００万円 × １０％ × １０年 ＝ ２００万円

複利運用の例

一方、複利運用では毎年受け取る１０％の利息を元金に組み入れていきます。

１年目に受け取った利息１０万円を元金に組み入れ１１０万円にします。
すると、２年目は１１０万円に対して１０％の利息がもらえますから、
１１０万円×１０％＝１１万円の利息がもらえる訳です。

単利の場合と比べ、１万円利息が増えました。

さらにこの受け取った利息１１万円を元金１１０万円に組み入れると、
元金は１２１万円になります。

３年目はこの１２１万円に対して利息がもらえます。
１２１万円×１０％＝１２.１万円の利息がもらえます。
利息を再投資しない単利と比べて２万１０００円利息が増えました。

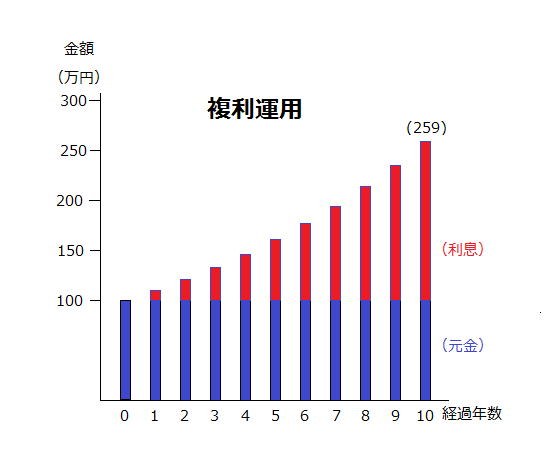
このように毎年利息を元金に組み入れ
再投資していくと、
１０年後には１００万円だった元金が
約２５９万円になります。

１００万円 × （１＋１０％）＾１０年 ≒ ２５９万円

同じ１０％で運用しても、
単利運用だと２００万円ですから、
５９万円もプラスで増やすことが
できた訳です。

着実に利息が得られる場合は
元金に再投資していく複利運用が
長期的に有利になっていくことが分かります。

複利の考え方をビジネスに応用すると…

では、この複利の考え方をビジネスに応用できないか、考えてみます。

コンビニやファーストフード店などのフランチャイズ店。

フランチャイズ店は、１つの成功する「システム」を開発し、
何をするべきかを詳細に記録し、
その「モデル」を他の誰にでも教えること（複製）ができるようにしました。

本部が得た営業ノウハウを使って、同じような店舗を複数作っていき、
これが大成功して急成長したのです。

しかし、この場合は一店舗ずつ一店舗ずつ、増えていきますので、
これは先に説明した単利運用の考え方になります。（直線的成長）

では、これに複利の考え方を取り入れたらどうなるでしょうか？

すなわち、各店舗がさらにその営業ノウハウを使って店舗を増やしていったら…
（これが、指数関数的成長）

なにかすごいことが起こりそうな予感がしませんか？

実は、このビジネス形態がすでに存在しています。
それが、ネットワークビジネス（ＭＬＭ）。

ネットワークビジネスは、
フランチャイズビジネスの長所（複製）を取り入れ、短所（高額な加盟金他）を排除し、
かつ直線的成長ではなく指数関数的成長が見込める最強のビジネスモデル。

小さなことでも積み重ねていけば、やがてそれは大きな財産になります。
複利の発想をすれば、成長は直線ではなく一気に上昇カーブを描くようになります。

常にわずかでもいいから今よりも成長していくことを意識してみましょう。

やらない手はないと思いますよ。

ネットワークビジネス成功戦略：無料メルマガ登録

私たちのグループで学んでいる成功マインドやビジネススキルを、
メルマガでご紹介しています。

ネットワークビジネスで本気で稼ぎたいとお考えの方、
無料で購読できますのでお気軽にご利用ください。

a:1194 t:1 y:0